rrBLUP

rrBLUP包简介

R 包rrBLUP能方便快速地实现RRBLUP(Ridge Regression Best Linear Unbiased Prediction)模型，该包主要有A.mat和mixed.solve两个核心函数。

A.mat

用法

A.mat函数用来过滤和填充基因型，返回加性效应关系矩阵（即Kinship）：

A.mat(  
X, #编码为{-1,0,1}的标记矩阵，可包含小数点（表明已填充过）和NA  
min.MAF=NULL, #最小等位基因频率  
max.missing=NULL, #最大缺失值比例  
impute.method="mean", #填充方法，mean/EM  
tol=0.02, #EM算法的收敛标准  
n.core=1, #EM算法的并行核心数（仅unix）  
shrink=FALSE, #收缩估计  
return.imputed=FALSE #返回填充标记矩阵  
)

参数

X	n个品系与m个双等位基因标记的非相基因型矩阵(n × m)，编码为{-1，0，1}。允许使用小数点(表明已填充过)和缺失值(NA)。
min.MAF	最小等位基因频率。A矩阵对稀有等位基因不敏感，因此默认情况下只删除单态标记。
max.missin	最大缺失值比例；默认完全删除丢失的标记
impute.method	有两种选择。默认值为“Mean”，表示每个标记的平均值。“EM”选项使用EM算法(请参阅详细信息)。
tol	指定EM算法的收敛标准(请参阅详细信息).
n.core	指定用于EM算法的并行核心数量(仅在UNIX命令行中使用)。
shrink	设置shrink=FALSE以禁用收缩估计。有关如何启用收缩估算的详细信息，请参阅。
return.imputed	如果为True，则返回计算的标记矩阵。

细节

在高密度标记矩阵中，关系矩阵被估计为 A = W W ′ c A=\frac{WW'}{c}A=cWW′,其中W i k = X i k + 1 − 2 p k W_{ik}=X_{ik}+1-2p_kWik=Xik+1−2pk，P k P_kPk是标记k的1个等位基因的频率。通过使用归一化常数c = 2 ∑ k p k ( 1 − p k ) c=2\sum_{k} p_k(1-p_k)c=2∑kpk(1−pk)，对角线元素的平均值为1 + f 1+f1+f1。
EM补偿算法基于多变量正态分布，设计用于GBS(genotyping-by-sequencing)标记，GBS倾向于高密度，但有大量缺失的数据2。当R M S e r r o r = n − 1 ∣ ∣ A t − A t − 1 ∣ ∣ 2 < t o l RMS error=n^{-1}||A_t-A_{t-1}||_2 <tolRMSerror=n−1∣∣At−At−1∣∣2<tol时，EM算法在迭代 t tt 处停止。
收缩估计可以提高全基因组标记辅助选择的准确性，特别是在低标记密度的情况下1。收缩强度的范围从0 00(无收缩)到1 ( A = ( 1 + f ) I ) 1 (A=(1+f)I)1(A=(1+f)I)。有两种算法可用于估计收缩强度。
- 第一个是Endelman和Jannink(2012)中描述的方法，由S h r i n k = l i s t ( m e t h o d = “ E J ” ) Shrink=list(method=“EJ”)Shrink=list(method=“EJ”)指定1。
- 第二种方法是将随机的标记样本指定为模拟QTL，然后基于QTL将A矩阵与基于剩余标记的A矩阵进行回归。3 4 回归方法由s h r i n k = l i s t ( m e t h o d = “ r e g ” ， n . q t l = 100 ， n . i t e r = 5 ) shrink=list(method=“reg”，n.qtl=100，n.iter=5)shrink=list(method=“reg”，n.qtl=100，n.iter=5)指定，其中参数n . q t l n.qtln.qtl和n . i t e r n.itern.iter可以分别调整模拟QTL的数量和迭代次数。
收缩和EM补偿选项是为相反的场景(低密度与高密度)设计的，不能同时使用。当使用EM算法时，推定的等位基因可以位于区间[-1，1]之外。不满足min.MAF和max.Missing标准的多态标记不被补偿。

值

如果 r e t u r n . i m p u t e d = F A L S E return.imputed = FALSEreturn.imputed=FALSE,返回 n × n n×nn×n 的加性关系矩阵
如果 r e t u r n . i m p u t e d = T R U E return.imputed = TRUEreturn.imputed=TRUE,该函数返回包含以下内容的列表
- $A – A矩阵
- $imputed – 补偿标记矩阵

GWAS

基于混合模型进行全基因组关联分析5：

$y = X β + Z g + S τ + ϵ y = X β + Z g + S τ + \e = X β + Z g + S τ + ϵ$

其中β \betaβ是固定效应向量，既可以对环境因素进行建模，也可以对群体结构进行建模。变量g gg将为每个株系的遗传背景建立以下具有随机效应的模型：V a r [ g ] = K σ 2 V_{ar}[g]=K\sigma^2Var[g]=Kσ2。变量τ \tauτ将加性SNP效应建模为固定效应。残差是：V a r [ ϵ ] = K σ e 2 V_{ar}[\epsilon]=K\sigma^2_eVar[ϵ]=Kσe2

用法

GWAS(pheno, geno, fixed=NULL, K=NULL, n.PC=0,min.MAF=0.05, n.core=1, P3D=TRUE, plot=TRUE)

参数

选项	意义
pheno	数据框，其中第一列是品种名(gid)。其余的列可以是表型，也可以是固定效果的级别。任何没有被指定为固定效应的列都被假定为表型。
geno	第一列中具有标记名称的数据框。第二列和第三列分别包含染色体和定位位置(bp或cm)，只有当plot=true时才使用它们来绘制曼哈顿图。如果标记未映射，只需为这两列使用占位符。列4和更高的列包含每行的分数，编码为{-1，0，1}={aa，Aa，AA}。允许使用小数(填充)和缺失(NA)值。列名必须与pheno数据框中的行名相匹配。
fixed	一个字符串数组，其中包含应作为(分类)固定效果包含在混合模型中的列的名称。
K	由于多基因效应导致的行间协方差的血缘关系矩阵。如果未通过，则使用A.mat从标记计算。
n.PC	要包含为固定效果的主分量数。默认值为0(等于K模型)。
min.MAF	指定最小次要等位基因频率(MAF)。如果有标记的MAF小于min.MAF，则为其分配零分。
n.core	设置n.core>1将在具有多核的计算机上启用并行执行(仅在UNIX命令行使用)。
P3D	当P3D=TRUE时，REML只估计方差分量一次，模型中没有任何标记。当P3D=FALSE时，通过REML分别估计每个标记的方差分量。
plot	当plot=TRUE时，生成QQ和曼哈顿图。

细节

对于表型来自不同环境的不平衡设计，可以使用fixed选项对环境平均值进行建模(例如，如果表型数据框中的列称为“env”，则fixed=“env”)。当包括主分量时(P+K模型)，载荷由K矩阵的特征值分解确定。
术语P3D(先前确定的总体参数)是由Zhang等人引入的6。当P3D=FALSE时，此函数等同于具有REML的EMMA7.当P3D=TRUE时，它等同于EMMAX8。与P3D=FALSE相比，P3D=TRUE选项速度更快，但可能低估了重要性。
曼哈顿图像中的虚线对应的是FDR=0.05，并且是使用qvalue包计算的9。通过插值确定对应于q-valu =0.05的p值。如果没有小于0.05的q值，则省略虚线。

值

返回一个数据框，其中前三列是标记名称、染色体和位置，后续列是性状的标记分数(− l o g 10 p −log_{10}p−log10p)。

kin.blup

用G-BLUP预测基因型值，其中基因型协方差G可以是加性的，也可以是基于高斯核的。

用法

kin.blup(data,geno,pheno,GAUSS=FALSE,K=NULL,fixed=NULL,covariate=NULL, PEV=FALSE,n.core=1,theta.seq=NULL)

参数

选项	意义
data	包含表型、基因型标识符和任何环境变量列的数据框。
geno	数据框中包含基因型标识符的列名的字符串。
pheno	数据框中包含表型的列名的字符串。
GAUSS	要使用高斯核对遗传协方差进行建模，请设置GAUSS=TRUE并传递K的欧几里德距离(见下文)。
K	有三个选项可用于指定亲属关系:1)如果 K = N U L L K=NULLK=NULL,基因型被认为是独立的(G = I V g G=IV_gG=IVg)；2)对于育种值预测，设置G A U S S = F A L S E GAUSS=FALSEGAUSS=FALSE并使用K KK的相加关系矩阵来创建模型(G = K V g G=K V_gG=KVg)；3）对于高斯内核，设置G A U S S = T R U E GAUSS=TRUEGAUSS=TRUE并传递K KK的欧几里得距离矩阵来创建模型G i j = e − ( K i j θ ) 2 V g G_{ij}=e^{-(\frac{K_{ij}} {\theta})^2}V_gGij=e−(θKij)2Vg
fixed	一个字符串数组，其中包含应作为(分类)固定效果包含在混合模型中的列的名称。
covariate	包含应作为协变量包含在混合模型中的列名的字符串数组。
PEV	当PEV=TRUE时，该函数返回遗传型值的预测误差方差（P E V i = V a r [ g i ∗ − g i ] PEV_i=V_{ar}[g_i^*-g_i]PEVi=Var[gi∗−gi]）
n.core	指定用于并行执行高斯内核方法的核心数量(仅用于UNIX命令行)。
theta.seq	高斯核的比例参数是通过最大化值网格上的受限对数似然率来设置的。默认情况下，栅格是通过将间隔( 0 ， m a x ( K ) ] (0，max(K)](0，max(K)]分割为 10个点来构建的。将数值数组传递给此变量(theta.seq=“theta Sequence”)将指定一组不同的网格点(例如，对于较大的问题，您可能希望少于10个)。

细节

此函数是Mixed.solve的包装器，从而求解以下形式的混合模型：

$y = X β + [Z 0] g + ϵ y = X β + [Z 0]_{g} + ϵ = X β + [Z 0] g + ϵ$

其中，β \betaβ是固定效应向量，g gg是具有协变量G = V a r [ g ] G=V_{ar}[g]G=Var[g]的随机表型值向量，残差为V a r [ ϵ i ] = R i σ e 2 V_{ar}[\epsilon_i]=R_i\sigma^2_eVar[ϵi]=Riσe2,默认R i = 1 R_i=1Ri=1。遗传值的设计矩阵已经被划分，以说明并不是所有的品系都需要表型(例如，对于基因组选择来说)。与mixed.solve不同，这一函数并不会返回固定效应的估计值，只返回基因型值的BLUP解。它的设计目的是取代kinship.BLUP，并使用户不必显式构造设计矩阵。方差分量由REML估计，并且为K中的每个条目返回BLUP值，无论它是否已有表型。K的行名必须与表现型系数据帧中的基因型标签相匹配;
丢失的表型(NA)被简单地省略了。
与它的前身不同，这个函数不直接处理标记数据。对于育种值的预测，用户必须提供一个关系矩阵，该矩阵可以从带有A.mat的标记中计算出来。对于高斯核预测，通过K的欧氏距离矩阵，它可以用dist来计算。
在混合模型的术语中，“固定”变量和“协变量”变量都是固定效应( 上式中的β \betaβ):前者被视为具有不同层次的因子，而后者是连续的，每个变量有一个系数。总体均值作为一个固定效应自动包括在内。预测误差方差(PEV)是BLUPs的SE的平方(见mix .solve)，可用于根据r i 2 = 1 − P E V i V g K i i r^2_i=1-\frac{PEV_i}{V_gK_{ii}}ri2=1−VgKiiPEVi估计BLUP预测的预期精度。

值

函数总是返回以下值：

$V g V_gVg	遗传方差的REML估计
$V e V_eVe	误差方差的REML估计
$g gg	遗传价值的BLUP值
$r e s i d residresid	残差
$p r e d predpred	预测的遗传值，平均于固定效应
IF P E V = T R U E PEV=TRUEPEV=TRUE,返回值也会包括$P E V PEVPEV
$P E V PEVPEV	遗传值的预测误差方差
if G A U S S = T R U E GAUSS=TRUEGAUSS=TRUE,返回值也会包括 $p r o f i l e profileprofile
$p r o f i l e profileprofile	高斯核中尺度参数的对数似然分布

mixed.solve

描述

计算方程的混合模型的最大似然(ML/REML)解
y = X β + Z u + ϵ y=X\beta+Zu+\epsilony=Xβ+Zu+ϵ
其中β \betaβ是固定效应向量，u uu是是具有协方差V a r [ u ] = K σ u 2 V_{ar}[u]=K\sigma^2_uVar[u]=Kσu2的随机效应向量；残差是V a r [ ϵ ] = I σ e 2 V_{ar}[\epsilon]=I\sigma_e^2Var[ϵ]=Iσe2。这类混合模型除了残差外，还有一个单一的方差成分，与岭回归有密切的关系(岭回归参数：λ = σ e 2 σ u 2 \lambda=\frac{\sigma_e^2}{\sigma_u^2}λ=σu2σe2)

使用方法

mixed.solve函数求解模型参数：

mixed.solve(  
y, #观测值  
Z=NULL, #随机效应矩阵  
K=NULL, #随机效应协变量矩阵  
X=NULL, #固定效应矩阵  
method="REML", #最大似然估计方法，ML/REML  
bounds=c(1e-09, 1e+09), #岭回归参数两元素边界  
SE=FALSE, #是否计算标准误  
return.Hinv=FALSE #是否H取逆，一般在GWAS中用，忽略之  
)

mixed.solve函数返回值（列表）：

- Vu：σ^2_u的估计值
- Ve：σ^2_e的估计值
- beta：BLUE(β)，即训练群表型均值
- u：BLUP(u)，即预测值
- LL：maximized log-likelihood（ML/REML值）

如果设了标准误参数，则会返回：

beta.SE：β标准误
u.SE：u^*-u

参数

y	观测值向量( n × 1 ) (n×1)(n×1),遗漏的值(NA)被省略，同时也是X和Z对应的行。
Z	随机效应的涉及矩阵( n × m ) (n×m)(n×m)，如果没有通过，假定为单位矩阵
K	随机效应的协方差矩阵( m × m ) (m×m)(m×m),一定是半正定义的。如果没有通过，则假定为单位矩阵。
X	固定效应的设计矩阵( m × m ) (m×m)(m×m),如果没有通过，则使用一个向量1来建模截距。X必须是全列秩(意味着是可估计的)。
method	指定是否使用完整(“ML”)或限制(“REML”)最大似然方法。
bounds	包含两个元素的数组，它们指定岭回归参数的上下边界。
SE	如果为真，则计算标准误差
return.Hinv	如果为真，函数返回H = Z K Z ′ + λ I H = ZKZ' + \lambda IH=ZKZ′+λI的逆函数。这对GWAS很有用。

细节

返回值

如果 S E = F A L S E SE=FALSESE=FALSE,函数返回值包括:

$V u V_uVu	σ u 2 \sigma^2_uσu2的估计值
$V e V_eVe	σ e 2 \sigma^2_eσe2的估计值
$b e t a betabeta	BLUE(β \betaβ)
$u uu	BLUEP(u)
$L L LLLL	最大化对数似然(完全或有限，取决于方法)

如果 S E = T R U E SE=TRUESE=TRUE,函数返回值包括:

$b e t a . S E beta.SEbeta.SE	β \betaβ的标准误差
$u . S E u.SEu.SE	u ∗ − u u^*-uu∗−u的标准误差

如果 r e t u r n . H i n v = T R U E return.Hinv=TRUEreturn.Hinv=TRUE,函数返回值包括:

$H i n v HinvHinv	H的逆函数

实操代码

教程代码

library(rrGBLUP)
Pheno <- as.matrix(read.table(file ="traits.txt", header=TRUE))
dim(Pheno)
Markers <- as.matrix(read.table(file="snp.txt"), header=F)
dim(Markers)
impute = A.mat(Markers,max.missing=0.5,impute.method="mean",return.imputed=T)
Markers_impute2 = impute$imputed


traits=1  
cycles=500  
accuracy = matrix(nrow=cycles, ncol=traits)
# 验证
for(r in 1:cycles) {
    train <- as.matrix(sample(1:96, 58))
    test <- setdiff(1:96, train)
    Pheno_train <- Pheno[train,]
    m_train <- Markers_impute2[train,]
    Pheno_valid <- Pheno[test,]
    m_valid <- Markers_impute2[test,]
    yield <- Pheno_train[,1]
    yield_answer <- mixed.solve(yield, Z=m_train, K=NULL, SE = FALSE, return.Hinv=FALSE)
    pred_yield_valid <- m_valid %*% as.matrix(yield_answer$u)
    pred_yield <- pred_yield_valid[,1] + yield_answer$beta
    # pred_yield  # 这句没必要吧
    yield_valid <- Pheno_valid[,1]
    accuracy[r,1] <- cor(pred_yield_valid, yield_valid, use="complete")
}

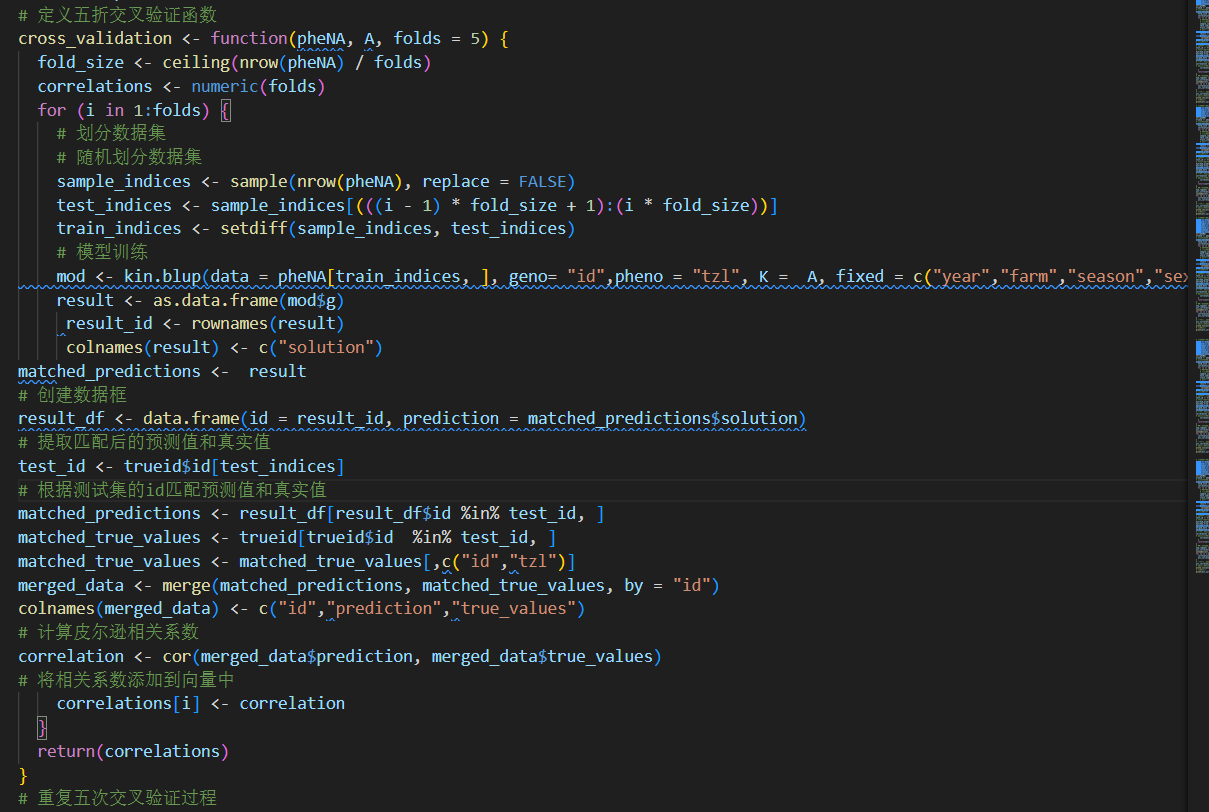
我的代码

traits_df <- read.csv(file ="p.csv", header=TRUE, stringsAsFactors=FALSE)
numeric_columns <- sapply(traits_df, is.numeric)
traits_matrix <- as.matrix(traits_df[, numeric_columns])
marker_matrix <- as.matrix(read.table(file="110k.txt"), header=F)
marker_matrix_imputed <- A.mat(marker_matrix,max.missing=0.5,impute.method="mean",return.imputed=T)
marker_matrix_imputed2 <- marker_matrix_imputed$imputed


# 假设 traits_matrix 和 marker_matrix_imputed2 已经被加载和定义
traits = 1
cycles = 10  # K-fold，这里K=10
accuracy = matrix(nrow=cycles, ncol=traits)

# 设置K-fold交叉验证
folds <- createFolds(traits_matrix[,3], k=cycles, list=TRUE, returnTrain=FALSE)

for(r in 1:length(folds)) {
    test_indices <- folds[[r]]
    train_indices <- setdiff(1:nrow(traits_matrix), test_indices)
    
    traits_train <- traits_matrix[train_indices,]
    marker_train <- marker_matrix_imputed2[train_indices,]
    traits_test <- traits_matrix[test_indices,]
    marker_test <- marker_matrix_imputed2[test_indices,]
    
    cw_train <- traits_train[,3]  # 假设第三列是你想要分析的性状
    cw_solve <- mixed.solve(cw_train, Z=marker_train, K=NULL, SE=FALSE, return.Hinv=FALSE)
    cw_pred_valid <- marker_test %*% as.matrix(cw_solve$u)
    cw_pred <- cw_pred_valid[,1] + as.vector(cw_solve$beta)
    cw_test <- traits_test[,3]
    
    accuracy[r,1] <- cor(cw_pred, cw_test, use="complete")
}

mean_accuracy <- mean(accuracy[,1])
print(mean_accuracy)